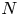Refine listing
Actions for selected content:
1418722 results in Open Access
Similarities and differences among selected gemmological varieties of chalcedony: chemistry, mineralogy and microstructure
-
- Journal:
- Mineralogical Magazine / Volume 88 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 136-146
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Selecting Out of “Politics”: The Self-Fulfilling Role of Conflict Expectation
-
- Journal:
- American Political Science Review / Volume 119 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 16 February 2024, pp. 40-55
- Print publication:
- February 2025
-
- Article
- Export citation
The Bilingualism Bonus in Socialist Slovenia: Domestic Policy or Diplomatic Prestige?
-
- Journal:
- Nationalities Papers / Volume 52 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 1375-1392
-
- Article
- Export citation
Green Innovation and Export Performance in Emerging Market Firms: A Legitimacy-based View
-
- Journal:
- Management and Organization Review / Volume 20 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 85-110
-
- Article
- Export citation
A wideband, thin, dual-negative, and polarization-independent square-tooth circular ring resonator-based metamaterial absorber for Ku-band applications
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 16 / Issue 6 / July 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 972-980
-
- Article
- Export citation
JLO volume 138 issue 3 Cover and Front matter
-
- Journal:
- The Journal of Laryngology & Otology / Volume 138 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. f1-f3
- Print publication:
- March 2024
-
- Article
-
- You have access
- Export citation
Weakly nonlinear analysis of thermoacoustic oscillations in can-annular combustors
-
- Journal:
- Journal of Fluid Mechanics / Volume 980 / 10 February 2024
- Published online by Cambridge University Press:
- 16 February 2024, A52
-
- Article
- Export citation
The American Political Science Review During the COVID-19 Pandemic
-
- Journal:
- PS: Political Science & Politics / Volume 57 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 427-434
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE UNIVERSAL THEORY OF THE HYPERFINITE II
 $_1$ FACTOR IS NOT COMPUTABLE
$_1$ FACTOR IS NOT COMPUTABLE
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 181-198
- Print publication:
- June 2024
-
- Article
- Export citation
Adherence to Mediterranean diet is inversely associated with depressive symptoms in older women: findings from the NutBrain Study
-
- Journal:
- British Journal of Nutrition / Volume 131 / Issue 11 / 14 June 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 1892-1901
- Print publication:
- 14 June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wideband millimeter-wave reflectarray antenna with reduced cross-polarization
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 16 / Issue 4 / May 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 636-644
-
- Article
- Export citation
Influence of parametric forcing on Marangoni instability
-
- Journal:
- Journal of Fluid Mechanics / Volume 981 / 25 February 2024
- Published online by Cambridge University Press:
- 16 February 2024, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Time Matters in Cross-Strait Relations: Tsai Ing-wen and Taiwan's Future
-
- Journal:
- The China Quarterly / Volume 259 / September 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 629-644
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Association of green tea consumption with prediabetes, diabetes and markers of glucose metabolism in rural Vietnam: a cross-sectional study
-
- Journal:
- British Journal of Nutrition / Volume 131 / Issue 11 / 14 June 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 1883-1891
- Print publication:
- 14 June 2024
-
- Article
-
- You have access
- HTML
- Export citation
From Musical Writings To Writing Music: Book-Writing Leading to Music School in Nineteenth-Century Calcutta
-
- Journal:
- Nineteenth-Century Music Review / Volume 21 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 492-517
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Care and Crisis: Making Beds in the National Health Service
-
- Journal:
- Journal of British Studies / Volume 63 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 349-371
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Molecular dynamics simulation of dodecyl dimethyl benzyl ammonium cation-intercalated montmorillonite
-
- Journal:
- Clay Minerals / Volume 58 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 16 February 2024, pp. 415-423
-
- Article
-
- You have access
- HTML
- Export citation
“Making the Peaks Higher”: Foundations of Stanford University’s Growth, 1910–1960
-
- Journal:
- Enterprise & Society / Volume 26 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 16 February 2024, pp. 218-248
- Print publication:
- March 2025
-
- Article
- Export citation
PSP volume 176 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. b1-b2
- Print publication:
- March 2024
-
- Article
-
- You have access
- Export citation
Donatella Montini and Irene Ranzato (eds.), The dialects of British English in fictional texts (Routledge Research in Language and Communication 10). Abingdon: Routledge, 2021. Pp. ix + 217. ISBN 9780367856115.
-
- Journal:
- English Language & Linguistics / Volume 28 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 413-419
-
- Article
- Export citation