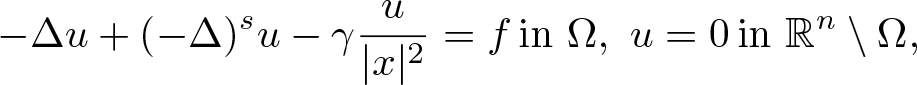Refine search
Actions for selected content:
25814 results in Abstract analysis
The nonabelian product modulo sum
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1069-1109
-
- Article
- Export citation
 $ \epsilon $-ISOMORPHISMS FOR RANK ONE
$ \epsilon $-ISOMORPHISMS FOR RANK ONE  $( \varphi , \Gamma )$-MODULES OVER LUBIN-TATE ROBBA RINGS
$( \varphi , \Gamma )$-MODULES OVER LUBIN-TATE ROBBA RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1895-1994
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pattern formation with jump discontinuity in a predator–prey model with Holling-II functional response
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1160-1182
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sobolev regularity of the inverse for minimizers of the neo-Hookean energy satisfying condition INV
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-21
-
- Article
- Export citation
On mixed local–nonlocal problems with Hardy potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-34
-
- Article
- Export citation
JMJ volume 24 issue 3 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. b1-b2
- Print publication:
- May 2025
-
- Article
-
- You have access
- Export citation
JMJ volume 24 issue 3 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. f1-f2
- Print publication:
- May 2025
-
- Article
-
- You have access
- Export citation
Maximal operators along flat curves with one variable vector field - Erratum
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 08 April 2025, p. 1421
-
- Article
-
- You have access
- HTML
- Export citation
Graph morphisms and exhaustion of curve graphs of low-genus surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 08 April 2025, pp. 1018-1068
-
- Article
- Export citation
Loop space decompositions of moment-angle complexes associated to two-dimensional simplicial complexes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 995-1017
-
- Article
- Export citation
On Growth Functions of Coxeter Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 979-993
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zero-one law of orbital limit points for weighted shifts
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 945-978
-
- Article
- Export citation
Rigidity of mapping class groups MOD powers of twists
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-71
-
- Article
- Export citation
Adversarial consistency and the uniqueness of the adversarial bayes classifier
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 04 April 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A hyperbolic free-by-cyclic group determined by its finite quotients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 500-502
- Print publication:
- September 2025
-
- Article
- Export citation
The Klein bottle has stably unbounded homeomorphism group
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 494-499
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Codazzi and totally umbilical hypersurfaces in
 $\mathrm {Sol}_1^4$
$\mathrm {Sol}_1^4$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 03 April 2025, pp. 487-493
- Print publication:
- September 2025
-
- Article
- Export citation
All, most, some? On diffeomorphisms of the interval that are distorted and/or conjugate to powers of themselves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 909-944
-
- Article
- Export citation
NLP verification: towards a general methodology for certifying robustness
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On some products of groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 869-897
-
- Article
- Export citation