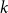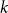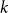Refine search
Actions for selected content:
9084 results in Discrete Mathematics, Information Theory and Coding
Hypergraphs without complete partite subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 11 December 2025, pp. 1-4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sidorenko’s conjecture for subdivisions and theta substitutions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 2 / March 2026
- Published online by Cambridge University Press:
- 10 December 2025, pp. 269-279
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On stability of rainbow matchings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 2 / March 2026
- Published online by Cambridge University Press:
- 09 December 2025, pp. 255-268
-
- Article
- Export citation
Conflict-free hypergraph matchings and coverings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 2 / March 2026
- Published online by Cambridge University Press:
- 04 December 2025, pp. 230-254
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Beyond the classification theorem of Cameron, Goethals, Seidel, and Shult
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 2 / March 2026
- Published online by Cambridge University Press:
- 28 November 2025, pp. 207-229
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Canonization of a random circulant graph by counting walks
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 2 / March 2026
- Published online by Cambridge University Press:
- 26 November 2025, pp. 178-206
-
- Article
- Export citation
A rainbow Dirac theorem for loose Hamilton cycles in hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 2 / March 2026
- Published online by Cambridge University Press:
- 11 November 2025, pp. 149-177
-
- Article
- Export citation
On higher dimensional point sets in general position
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 03 November 2025, pp. 134-148
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Powers of Hamilton cycles in oriented and directed graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 28 October 2025, pp. 101-133
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Disperse hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 27 October 2025, pp. 89-100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on the computational complexity of weak saturation
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 16 October 2025, pp. 83-88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random embeddings of bounded-degree trees with optimal spread
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 13 October 2025, pp. 71-82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Beyond the broken tetrahedron
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 10 October 2025, pp. 59-70
-
- Article
- Export citation
Saturation in random hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 07 October 2025, pp. 40-58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Comparing the sets of volume polynomials and Lorentzian polynomials
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 19 September 2025, pp. 26-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Glauber dynamics for the hard-core model on bounded-degree
 $H$-free graphs
$H$-free graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 19 September 2025, pp. 803-814
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An explicit economical additive basis
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 12 September 2025, pp. 815-820
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proper minor-closed classes of graphs have Assouad–Nagata dimension 2
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On approximability of satisfiable
 $\boldsymbol {k}$-CSPs: II
$\boldsymbol {k}$-CSPs: II
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 20 August 2025, pp. 857-926
-
- Article
- Export citation
Embedding nearly spanning trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 11 August 2025, pp. 927-931
-
- Article
- Export citation