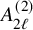Refine listing
Actions for selected content:
231 results in 05Exx
POWERS OF FACET IDEALS OF SIMPLICIAL TREES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 18 December 2025, e9
- Print publication:
- 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Borel-type presentation of the torus-equivariant quantum K-ring of flag manifolds of type C
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 December 2025, e198
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Free fermionic probability theory and k-theoretic schubert calculus
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 09 December 2025, e197
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on transverse sets and bilinear varieties
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 27 November 2025, pp. 1-13
-
- Article
- Export citation
Unimodular valuations beyond Ehrhart
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 November 2025, e188
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A GEOMETRIC APPROACH TO POLYNOMIAL PROPERTY FOR PATTERN SUBGROUPS IN
 ${{\mathrm {\mathbf {U}}}}_{\boldsymbol {a,b,c,d}}$
${{\mathrm {\mathbf {U}}}}_{\boldsymbol {a,b,c,d}}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 19 November 2025, pp. 1-18
-
- Article
- Export citation
Rational Delsarte designs and Galois fusions of association schemes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 18 November 2025, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PERFECT CODES IN THE HOMOGENEOUS METRIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 30 October 2025, pp. 1-9
-
- Article
- Export citation
Equivariant Ehrhart theory of hypersimplices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 27 October 2025, e178
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on the computational complexity of weak saturation
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 16 October 2025, pp. 1-6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Procesi bundle over the Γ-fixed points of the Hilbert scheme of points in
 $\mathbb{C}^2$
$\mathbb{C}^2$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probabilistic operators for non-attacking tableaux and a compact formula for the symmetric Macdonald polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 September 2025, e146
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantum K theory of Grassmannians, Wilson line operators and Schur bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 04 September 2025, e140
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A conditional lower bound for the Turán number of spheres
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 11 August 2025, pp. 848-856
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Regularity and multiplicity of Veronese type algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Colored interacting particle systems on the ring: Stationary measures from Yang–Baxter equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1855-1922
- Print publication:
- August 2025
-
- Article
- Export citation
Ideals and their Fitting ideals
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 30 July 2025, pp. 609-621
- Print publication:
- November 2025
-
- Article
- Export citation
ENUMERATION AND DIVISIBILITY OF HIGHER DIMENSIONAL KING WALKS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-12
-
- Article
- Export citation
Posets arising from decompositions of objects in a monoidal category
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 July 2025, e123
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth locus of twisted affine Schubert varieties and twisted affine Demazure modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 July 2025, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation