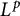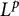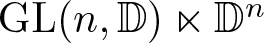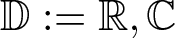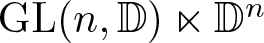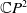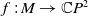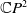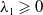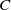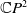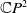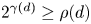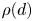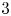Refine listing
Actions for selected content:
115 results in 53Axx
Petty projection inequality on the sphere and on the hyperbolic space
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 August 2025, pp. 1-28
-
- Article
- Export citation
Conformally Kähler structures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maximal surfaces in the Lorentzian Heisenberg group
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 29 July 2025, pp. 579-608
- Print publication:
- November 2025
-
- Article
- Export citation
Lower bounds on density for topologically nontrivial minimal cones up to dimension six
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 21 July 2025, e122
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characters and transfer maps via categorified traces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 June 2025, e93
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A strong Frankel theorem for shrinkers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 19 August 2025, pp. 947-958
- Print publication:
- May 2025
-
- Article
- Export citation
Invariant divisors and equivariant line bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 April 2025, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPLETE HYPERSURFACES WITH LINEARLY RELATED HIGHER ORDER MEAN CURVATURES IN THE HYPERBOLIC SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 82-105
- Print publication:
- August 2025
-
- Article
- Export citation
Elliptic Pre-Complexes, Hodge-like Decompositions and Overdetermined Boundary-Value Problems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 March 2025, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Special homogeneous surfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 2 / September 2024
- Published online by Cambridge University Press:
- 22 October 2024, pp. 333-362
- Print publication:
- September 2024
-
- Article
- Export citation
EXCEPTIONAL SIMPLE REAL LIE ALGEBRAS
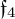 $\mathfrak {f}_4$ AND
$\mathfrak {f}_4$ AND 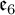 $\mathfrak {e}_6$ VIA CONTACTIFICATIONS
$\mathfrak {e}_6$ VIA CONTACTIFICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 July 2024, pp. 157-201
- Print publication:
- January 2025
-
- Article
- Export citation
The geometry of C1,α flat isometric immersions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Catenaries and minimal surfaces of revolution in hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Index estimates of compact hypersurfaces in smooth metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1895-1913
- Print publication:
- October 2025
-
- Article
- Export citation
Spectral theory of the invariant Laplacian on the disk and the sphere – a complex analysis approach
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 01 March 2024, pp. 940-974
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Anisotropic flow, entropy, and
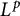 $L^p$-Minkowski problem
$L^p$-Minkowski problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1-20
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reversibility of affine transformations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 08 November 2023, pp. 1217-1228
-
- Article
- Export citation
A Helfrich functional for compact surfaces in
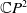 $\mathbb{C}P^{2}$
$\mathbb{C}P^{2}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 04 October 2023, pp. 36-50
- Print publication:
- January 2024
-
- Article
- Export citation
A note about charts built by Eriksson-Bique and Soultanis on metric measure spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 09 June 2023, pp. 49-59
- Print publication:
- March 2024
-
- Article
- Export citation
On inscribed trapezoids and affinely 3-regular maps
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 1024-1032
- Print publication:
- August 2024
-
- Article
- Export citation


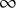

























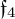
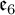













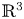
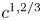
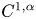
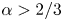
 of the “complexified unit circle”
of the “complexified unit circle”