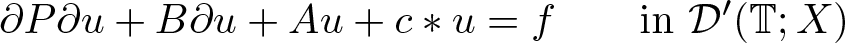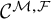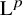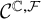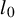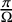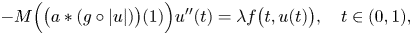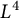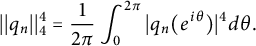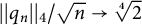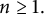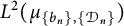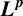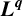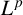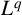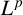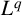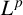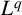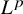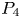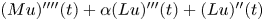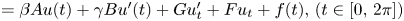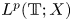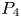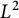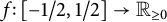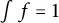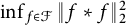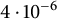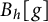Refine listing
Actions for selected content:
97 results in 42Axx
Large Salem sets avoiding nonlinear configurations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 November 2025, pp. 1-46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Hilbert space derived from the Weil distribution
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A unified topological analysis of variable growth Kirchhoff-type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Diophantine approximations with restrained denominators. Balance condition on decay and growth rates
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-36
-
- Article
- Export citation
The boundedness of the bilinear fractional integrals along curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 22 August 2025, pp. 1-31
-
- Article
- Export citation
A CRITERION FOR ENSURING POSITIVITY OF FOURIER TRANSFORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 August 2025, pp. 1-11
-
- Article
- Export citation
The invariant subspaces of periodic Fourier multipliers with application to abstract evolution equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1-47
-
- Article
- Export citation
ON SOME EFFECTIVE RESULTS INVOLVING ZEROS OF THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 21 March 2025, pp. 563-565
- Print publication:
- June 2025
-
- Article
-
- You have access
- HTML
- Export citation
Parametric Fourier and Mellin transforms of power-constructible functions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 29 November 2024, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A mathematical theory of super-resolution and two-point resolution
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 October 2024, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A unified characterization of convolution coefficients in nonlocal differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-19
-
- Article
- Export citation
Almost sure convergence of the
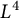 $L^4$ norm of Littlewood polynomials
$L^4$ norm of Littlewood polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 872-885
- Print publication:
- September 2024
-
- Article
- Export citation
Tree structure of spectra of spectral Moran measures with consecutive digits
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 593-610
- Print publication:
- September 2024
-
- Article
- Export citation
QUALITATIVE UNCERTAINTY PRINCIPLE ON CERTAIN LIE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 289-307
- Print publication:
- June 2024
-
- Article
- Export citation
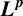 $\boldsymbol {L}^{\boldsymbol {p}}$–
$\boldsymbol {L}^{\boldsymbol {p}}$–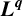 $\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
$\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 18 October 2023, pp. 375-395
- Print publication:
- December 2023
-
- Article
- Export citation
On a multi-parameter variant of the Bellow–Furstenberg problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 September 2023, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Periodic solutions of four-order degenerate differential equations with finite delay in vector-valued function spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 14 September 2023, pp. 395-412
- Print publication:
- April 2025
-
- Article
- Export citation
Remarks on countable subadditivity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 23 August 2023, pp. 1504-1517
- Print publication:
- October 2024
-
- Article
- Export citation
An optimal
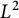 $L^2$ autoconvolution inequality
$L^2$ autoconvolution inequality
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 108-121
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPECTRAL MULTIPLIER THEOREMS FOR ABSTRACT DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 343-344
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation