Refine listing
Actions for selected content:
2845 results in 11xxx
The finite forms of MacMahon’s q-series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 02 January 2026, pp. 1-28
-
- Article
- Export citation
 $\Omega$-results for exponential sums related to Maass cusp forms for
$\Omega$-results for exponential sums related to Maass cusp forms for 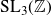 $\mathrm{SL}_3(\mathbb Z)$
$\mathrm{SL}_3(\mathbb Z)$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 29 December 2025, pp. 1-54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hybrid subconvexity for Maass form symmetric-square L-functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 December 2025, pp. 1-51
-
- Article
- Export citation
Equidistribution for nilsequences along spheres over finite fields
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 29 December 2025, pp. 1-73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Disintegration results for fractal measures and applications to Diophantine approximation
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 23 December 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On averages of completely multiplicative functions over co-prime integer pairs
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 19 December 2025, pp. 1-14
-
- Article
- Export citation
COHOMOLOGY OF THE BASIC UNRAMIFIED PEL UNITARY RAPOPORT-ZINK SPACE OF SIGNATURE
 $(1,n-1)$
$(1,n-1)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 18 December 2025, pp. 1-59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A PROBLEM OF NATHANSON ON NONMINIMAL ADDITIVE COMPLEMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 15 December 2025, pp. 1-8
-
- Article
- Export citation
Likely intersections
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 December 2025, e199
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dual p-adic Diophantine approximation on manifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 December 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NOTES ON GENERALISED INTEGRAL POLYNOMIAL PELL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 09 December 2025, pp. 1-13
-
- Article
- Export citation
Quantitative bounds in a popular polynomial Szemerédi theorem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 December 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A threshold for Poisson behavior of non-stationary product measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Explicit sumset sizes in additive number theory
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-12
-
- Article
-
- You have access
- HTML
- Export citation
Distribution of integers with digit restrictions via Markov chains
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conditional lower bounds on the distribution of central values: The case of modular forms
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-30
-
- Article
-
- You have access
- HTML
- Export citation
NONCOMMUTATIVE IWASAWA THEORY OF ABELIAN VARIETIES OVER GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-35
-
- Article
- Export citation
GENERALISED MAZUR’S GROWTH NUMBER CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 November 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON SOME QUADRATICS AND CUBICS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 November 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on transverse sets and bilinear varieties
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 27 November 2025, pp. 1-13
-
- Article
- Export citation