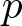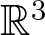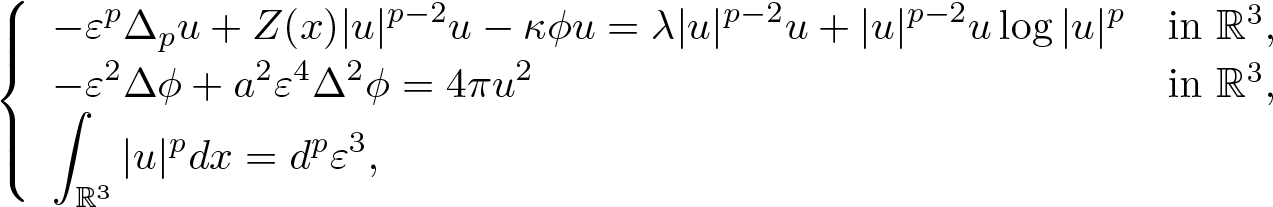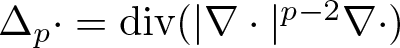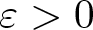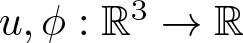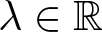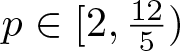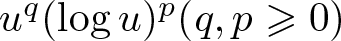Refine listing
Actions for selected content:
415 results in 35Jxx
MULTIPLE SOLUTIONS FOR QUASILINEAR SCHRÖDINGER EQUATIONS WITH NONLINEARITY SUBLINEAR AT ZERO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 26 January 2026, pp. 1-13
-
- Article
- Export citation
Superlinear problems involving nonlinear superposition operators of mixed fractional order
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 January 2026, pp. 1-26
-
- Article
- Export citation
Multiplicative Jensen’s formula and quantitative global theory of one-frequency Schrödinger operators
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 14 / 2026
- Published online by Cambridge University Press:
- 09 January 2026, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence and concentration of normalized solutions for logarithmic Schrödinger–Bopp–Podolsky type system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 December 2025, pp. 1-39
-
- Article
- Export citation
Liouville-type theorems for the quasilinear elliptic equation and inequality with logarithmic nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2025, pp. 1-15
-
- Article
- Export citation
Uniqueness of solution for logarithm Choquard equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2025, pp. 1-29
-
- Article
- Export citation
On approximation of convex functionals with a convexity constraint and general Lagrangians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 19 November 2025, pp. 1-17
-
- Article
- Export citation
Normalized solutions for p-Laplacian equation with general nonlinearities on bounded domain
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 November 2025, pp. 1-31
-
- Article
- Export citation
Existence and uniqueness of a positive solution to a rapidly growing problem via sub-supersolution method
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 November 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlocal carrier’s double phase problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 November 2025, pp. 1-24
-
- Article
- Export citation
Liouville theorems for the static Schrodinger equations with van der Waals type potentials
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 05 November 2025, pp. 1-27
-
- Article
- Export citation
Existence and symmetry breaking results for a Hénon-type equation with Grushin operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 November 2025, pp. 1-19
-
- Article
- Export citation
Non-degeneracy and local uniqueness of bubbling solutions for fractional almost critical problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-45
-
- Article
- Export citation
Concentration behavior of normalized ground states for mass critical Kirchhoff equations in bounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-44
-
- Article
- Export citation
Normalized multi-bump solutions of nonlinear Hartree equation with steep potential well
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 October 2025, pp. 1-37
-
- Article
- Export citation
A k-Hessian equation with a power nonlinearity source and self-similarity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-25
-
- Article
- Export citation
Harmonic exponential terms are polynomial
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 09 October 2025, pp. 1-6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Schwartz very weak solutions for Schrödinger type equations with distributional coefficients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 September 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimization of the principal eigenvalue of the Neumann Laplacian with indefinite weight and monotonicity of minimizers in cylinders
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth solutions to the Christoffel–Minkowski problem in hyperbolic space
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-29
-
- Article
- Export citation