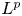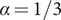Refine search
Actions for selected content:
52379 results in Statistics and Probability
Quantum computing for data-centric engineering and science
-
- Journal:
- Data-Centric Engineering / Volume 3 / 2022
- Published online by Cambridge University Press:
- 02 December 2022, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On mixed fractional stochastic differential equations with discontinuous drift coefficient
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 589-606
- Print publication:
- June 2023
-
- Article
- Export citation
Exponential ergodicity for a class of Markov processes with interactions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 465-478
- Print publication:
- June 2023
-
- Article
- Export citation
A defined benefit pension plan model with stochastic salary and heterogeneous discounting
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 62-83
- Print publication:
- January 2023
-
- Article
- Export citation
Neural modal ordinary differential equations: Integrating physics-based modeling with neural ordinary differential equations for modeling high-dimensional monitored structures
-
- Journal:
- Data-Centric Engineering / Volume 3 / 2022
- Published online by Cambridge University Press:
- 29 November 2022, e34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tsallis value-at-risk: generalized entropic value-at-risk
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 29 November 2022, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Managing the risk of mortality shocks
-
- Journal:
- Annals of Actuarial Science / Volume 16 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 29 November 2022, pp. 425-427
-
- Article
-
- You have access
- HTML
- Export citation
How actuarial perspectives can help in a pandemic
-
- Journal:
- Annals of Actuarial Science / Volume 16 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 29 November 2022, pp. 428-429
-
- Article
-
- You have access
- HTML
- Export citation
A simple European option pricing formula with a skew Brownian motion
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 29 November 2022, pp. 1029-1034
-
- Article
-
- You have access
- HTML
- Export citation
On random walks and switched random walks on homogeneous spaces
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 28 November 2022, pp. 398-421
-
- Article
- Export citation
PolicyCLOUD: A prototype of a cloud serverless ecosystem for policy analytics
-
- Journal:
- Data & Policy / Volume 4 / 2022
- Published online by Cambridge University Press:
- 28 November 2022, e44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Micro-level network dynamics of scientific collaboration and impact: Relational hyperevent models for the analysis of coauthor networks
-
- Journal:
- Network Science / Volume 11 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 28 November 2022, pp. 5-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Virtual sensing in an onshore wind turbine tower using a Gaussian process latent force model
- Part of
-
- Journal:
- Data-Centric Engineering / Volume 3 / 2022
- Published online by Cambridge University Press:
- 28 November 2022, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Changes in soil hydraulic properties due to organic amendment
-
- Journal:
- Experimental Results / Volume 3 / 2022
- Published online by Cambridge University Press:
- 28 November 2022, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Exponential Families in Theory and Practice
-
- Published online:
- 25 November 2022
- Print publication:
- 15 December 2022
Combining antibody markers for serosurveillance of SARS-CoV-2 to estimate seroprevalence and time-since-infection – CORRIGENDUM
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 25 November 2022, e188
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Connecting theory of plasmoid-modulated reconnection to observations of solar flares
-
- Journal:
- Experimental Results / Volume 3 / 2022
- Published online by Cambridge University Press:
- 25 November 2022, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Supercritical site percolation on the hypercube: small components are small
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 422-427
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modelling mortality: A bayesian factor-augmented var (favar) approach
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 29-61
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Forecasting mortality rates with a coherent ensemble averaging approach
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 2-28
- Print publication:
- January 2023
-
- Article
- Export citation