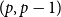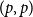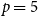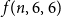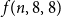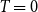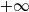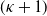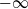Refine search
Actions for selected content:
52379 results in Statistics and Probability
Optimal allocation of policy limits in layer reinsurance treaties
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 24 November 2022, pp. 546-566
-
- Article
- Export citation
Ermanno Pitacco (1947–2022)
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 24 November 2022, p. 1
- Print publication:
- January 2023
-
- Article
-
- You have access
- HTML
- Export citation
New upper bounds for the Erdős-Gyárfás problem on generalized Ramsey numbers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 24 November 2022, pp. 349-362
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Efficiently generating geometric inhomogeneous and hyperbolic random graphs
-
- Journal:
- Network Science / Volume 10 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 23 November 2022, pp. 361-380
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Is the Capabilities Approach operationalizable to analyse the impact of digital identity on human lives
-
- Journal:
- Data & Policy / Volume 4 / 2022
- Published online by Cambridge University Press:
- 23 November 2022, e43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Understanding collaboration patterns on funded research projects: A network analysis
-
- Journal:
- Network Science / Volume 11 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 143-173
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ECT volume 38 issue 5 Cover and Front matter
-
- Journal:
- Econometric Theory / Volume 38 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 22 November 2022, pp. f1-f2
-
- Article
-
- You have access
- Export citation
ECT volume 38 issue 5 Cover and Back matter
-
- Journal:
- Econometric Theory / Volume 38 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 22 November 2022, pp. b1-b2
-
- Article
-
- You have access
- Export citation
GUEST EDITORS’ INTRODUCTION PART ONE: SPECIAL DUAL ISSUE OF ECONOMETRIC THEORY ON YALE 2018 CONFERENCE IN HONOR OF PETER C. B. PHILLIPS
-
- Journal:
- Econometric Theory / Volume 38 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 22 November 2022, pp. 841-844
-
- Article
- Export citation
COVID-19 and the effectiveness of ERM frameworks
-
- Journal:
- British Actuarial Journal / Volume 27 / 2022
- Published online by Cambridge University Press:
- 22 November 2022, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mean residual life order among largest order statistics arising from resilience-scale models with reduced scale parameters
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 72-85
-
- Article
- Export citation
Asset allocation for a DC pension plan with minimum guarantee constraint and hidden Markov regime-switching
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 37 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 21 November 2022, pp. 1035-1062
-
- Article
- Export citation

Dicing with Death
- Living by Data
-
- Published online:
- 18 November 2022
- Print publication:
- 08 December 2022
Time-convergent random matrices from mean-field pinned interacting eigenvalues
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 November 2022, pp. 394-417
- Print publication:
- June 2023
-
- Article
- Export citation
Has COVID-19 suppressed dengue transmission in Nepal?
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 18 November 2022, e196
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mathematical model and stability analysis on the transmission dynamics of skin sores
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 18 November 2022, e207
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
UEFA Euro 2020: lessons from the first multi-city international mass gathering during the COVID-19 pandemic
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 17 November 2022, e182
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The survival of epidemic and sporadic MRSA on human skin mimics is determined by both host and bacterial factors
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 16 November 2022, e203
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bi-national outbreak of Salmonella Newport infections linked to onions: the United States experience
-
- Journal:
- Epidemiology & Infection / Volume 150 / 2022
- Published online by Cambridge University Press:
- 16 November 2022, e199
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On moments of downward passage times for spectrally negative Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 16 November 2022, pp. 452-464
- Print publication:
- June 2023
-
- Article
- Export citation