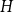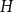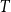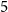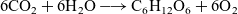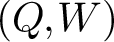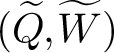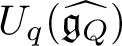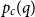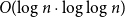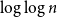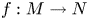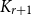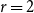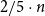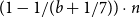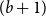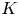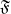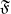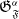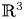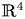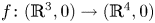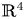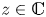Refine search
Actions for selected content:
25839 results in Abstract analysis
On tripartite common graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 25 May 2022, pp. 907-923
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the derivative of a polynomial
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 24 May 2022, pp. 303-310
-
- Article
- Export citation
On the sum of chemical reactions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 24 May 2022, pp. 303-325
-
- Article
- Export citation
EXTENSION BETWEEN SIMPLE MODULES OF PRO-p-IWAHORI HECKE ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 20 May 2022, pp. 2775-2804
- Print publication:
- November 2023
-
- Article
- Export citation
LOG-TRANSFORM AND THE WEAK HARNACK INEQUALITY FOR KINETIC FOKKER-PLANCK EQUATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 16 May 2022, pp. 2749-2774
- Print publication:
- November 2023
-
- Article
- Export citation
The diameter of the uniform spanning tree of dense graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 13 May 2022, pp. 1010-1030
-
- Article
- Export citation
A distributionally ambiguous two-stage stochastic approach for investment in renewable generation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 12 May 2022, pp. 484-504
-
- Article
- Export citation
Fractional interpolation inequality and radially symmetric ground states
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 12 May 2022, pp. 937-957
- Print publication:
- June 2023
-
- Article
- Export citation
CATEGORICAL AND K-THEORETIC HALL ALGEBRAS FOR QUIVERS WITH POTENTIAL
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 11 May 2022, pp. 2717-2747
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The critical mean-field Chayes–Machta dynamics
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 11 May 2022, pp. 924-975
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compact and weakly compact Lipschitz operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 11 May 2022, pp. 1002-1020
- Print publication:
- June 2023
-
- Article
- Export citation
THE HITCHIN CONNECTION IN ARBITRARY CHARACTERISTIC
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 11 May 2022, pp. 449-492
- Print publication:
- January 2023
-
- Article
- Export citation
The chromatic profile of locally colourable graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 10 May 2022, pp. 976-1009
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Delta-invariants of complete intersection log del Pezzo surfaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. 1021-1036
- Print publication:
- June 2023
-
- Article
- Export citation
Characterization of totally geodesic foliations with integrable and parallelizable normal bundle
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. 128-137
-
- Article
- Export citation
Casting light on shadow Somos sequences
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. S87-S101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The dual tree of a fold map germ from $\mathbb {R}^{3}$
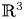 to $\mathbb {R}^{4}$
to $\mathbb {R}^{4}$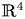
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 06 May 2022, pp. 958-977
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral representation of hydraulic permeability
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 06 May 2022, pp. 907-936
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distribution of tree parameters by martingale approach
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 29 April 2022, pp. 737-764
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic and transient dynamics of SEIR epidemic models on weighted networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 26 April 2022, pp. 238-261
-
- Article
- Export citation