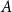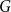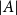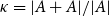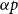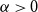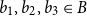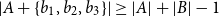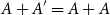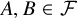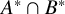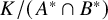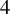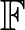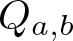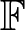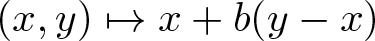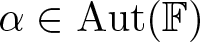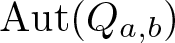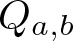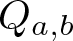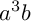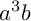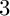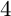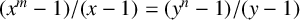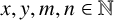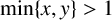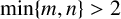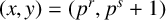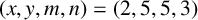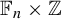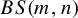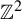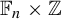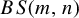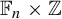Refine listing
Actions for selected content:
152 results in 05Bxx
Rational Delsarte designs and Galois fusions of association schemes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 18 November 2025, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the existence of reflecting n-queens configurations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 October 2025, e169
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal Kinematics on
 $\mathcal{M}_{0,n}$
$\mathcal{M}_{0,n}$
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Orthogonal matroids over tracts
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 August 2025, e130
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local generation of tilings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 18 July 2025, pp. 3377-3418
- Print publication:
- November 2025
-
- Article
- Export citation
On off-diagonal Ramsey numbers for vector spaces over
 $\mathbb{F}_{2}$
$\mathbb{F}_{2}$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 25 June 2025, pp. 503-518
- Print publication:
- September 2025
-
- Article
- Export citation
Supersolvability of built lattices and Koszulness of generalized Chow rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1284-1312
- Print publication:
- June 2025
-
- Article
- Export citation
The operad of Latin hypercubes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 475-486
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal H-factors and covers
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 14 February 2025, pp. 136-152
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXISTENCE OF K-MULTIMAGIC SQUARES AND MAGIC SQUARES OF kth POWERS WITH DISTINCT ENTRIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 441-448
- Print publication:
- December 2025
-
- Article
- Export citation
Face enumeration for split matroid polytopes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 07 February 2025, pp. 528-544
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounded Littlewood identity related to alternating sign matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 December 2024, e124
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPLEX WEIGHING MATRICES AND QUATERNARY CODES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 22 October 2024, pp. 14-22
- Print publication:
- August 2025
-
- Article
- Export citation
Small subsets with large sumset: Beyond the Cauchy–Davenport bound
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 21 February 2024, pp. 411-431
-
- Article
- Export citation
A question of Frohardt on
 $2$-groups, skew translation quadrangles of even order and cyclic STGQs
$2$-groups, skew translation quadrangles of even order and cyclic STGQs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 December 2023, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isomorphisms of quadratic quasigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 24 November 2023, pp. 1085-1109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stellahedral geometry of matroids
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 09 October 2023, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TILINGS OF THE SPHERE BY CONGRUENT QUADRILATERALS II: EDGE COMBINATION
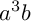 $a^3b$ WITH RATIONAL ANGLES
$a^3b$ WITH RATIONAL ANGLES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 07 September 2023, pp. 128-163
- Print publication:
- March 2024
-
- Article
- Export citation
A NOTE ON THE GOORMAGHTIGH EQUATION CONCERNING DIFFERENCE SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 443-452
- Print publication:
- June 2024
-
- Article
- Export citation
Strongly aperiodic SFTs on generalized Baumslag–Solitar groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 20 June 2023, pp. 1209-1238
- Print publication:
- May 2024
-
- Article
- Export citation