Refine listing
Actions for selected content:
1073 results in 05Cxx
Large and moderate deviations in Poisson navigations
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 10 September 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The distance on the slightly supercritical random series–parallel graph
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proper minor-closed classes of graphs have Assouad–Nagata dimension 2
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RAMSEY NUMBERS OF CYCLES VERSUS MULTIPLE ODD WHEELS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-9
-
- Article
- Export citation
On the f-vectors of flow polytopes for the complete graph
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Contiguity and remote contiguity of some random graphs
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 19 August 2025, pp. 1-18
-
- Article
- Export citation
Graphes dans les surfaces et ergodicité topologique
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-42
-
- Article
- Export citation
Embedding nearly spanning trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 11 August 2025, pp. 927-931
-
- Article
- Export citation
A stability theorem for multi-partite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 11 August 2025, pp. 821-847
-
- Article
- Export citation
A conditional lower bound for the Turán number of spheres
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 11 August 2025, pp. 848-856
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REVERSE MATHEMATICS OF A UNIFORM KRUSKAL–FRIEDMAN THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modified ascent sequences avoiding a pattern of length 4
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1390-1418
-
- Article
- Export citation
MEASURABLE DOMATIC PARTITIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-25
-
- Article
- Export citation
Online matching for the multiclass stochastic block model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1360-1381
- Print publication:
- December 2025
-
- Article
- Export citation
Mutation graph of support
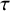 $\tau $-tilting modules over a skew-gentle algebra
$\tau $-tilting modules over a skew-gentle algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Ceresa period from tropical homology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting independent sets in structured graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 07 July 2025, pp. 625-634
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THREE ALGORITHMIC APPROACHES TO THE GENERAL POSITION PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 113 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-9
- Print publication:
- February 2026
-
- Article
- Export citation
NONASSORTATIVE COMMUNITY STRUCTURES IN COMPLEX NETWORKS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 04 July 2025, pp. 561-562
- Print publication:
- December 2025
-
- Article
-
- You have access
- HTML
- Export citation
A large deviation principle for block models
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 680-753
-
- Article
- Export citation