Refine listing
Actions for selected content:
428 results in 46Lxx
A PANORAMIC VIEW OF GROUPOIDS AND MRAs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 12 January 2026, pp. 1-48
-
- Article
- Export citation
DETECTING IDEALS IN REDUCED CROSSED PRODUCT C*-ALGEBRAS OF TOPOLOGICAL DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 16 December 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Support of the Brown measure of a family of free multiplicative Brownian motions with non-negative initial condition
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 December 2025, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Von Neumann orbit equivalence
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 December 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized Meixner-type free gamma distributions: Convolution formulas and potential correspondence
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 November 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ideal structure of uniform Roe algebras: beyond Property A
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inclusions of operator algebras from tensor categories: beyond irreducibility
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trace spaces of full free product
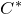 $C^*$-algebras
$C^*$-algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 07 January 2026, pp. 2947-2989
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EMBEDDABILITY OF HIGHER-RANK GRAPHS IN GROUPOIDS AND THE STRUCTURE OF THEIR
 $\mathbf {C^*}$-ALGEBRAS
$\mathbf {C^*}$-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 31 October 2025, pp. 314-346
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MORPHISMS OF CUNTZ–PIMSNER ALGEBRAS FROM COMPLETELY POSITIVE MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 31 October 2025, pp. 274-313
-
- Article
- Export citation
COACTIONS OF COMPACT GROUPS ON Mn
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 31 October 2025, pp. 418-435
-
- Article
- Export citation
DEFORMATION OF FELL BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 31 October 2025, pp. 347-381
-
- Article
- Export citation
A central limit theorem for partial transposes of multipartite Wishart matrices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 September 2025, pp. 1-38
-
- Article
- Export citation
PROPERTY (T) AND STRONG 1-BOUNDEDNESS FOR VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-34
-
- Article
- Export citation
Simplicity of crossed products by FC-hypercentral groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 28 October 2025, pp. 2272-2319
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON TOEPLITZ ALGEBRAS OF PRODUCT SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 26 August 2025, pp. 436-463
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Operator realizations of non-commutative analytic functions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 August 2025, e137
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-invariant lifts of completely positive maps for groupoid actions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 19 August 2025, pp. 35-63
- Print publication:
- January 2026
-
- Article
- Export citation
Semigroups of self-similar actions and higher rank Baumslag–Solitar semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 August 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local topological order and boundary algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 August 2025, e135
-
- Article
-
- You have access
- Open access
- HTML
- Export citation







 -groupoid algebras to the general twisted setting.
-groupoid algebras to the general twisted setting.