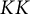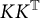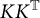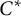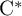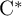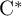Refine listing
Actions for selected content:
181 results in 19xxx
Toric arc schemes and q-enumeration of lattice points
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 December 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
VORONOI COMPLEXES IN HIGHER DIMENSIONS, COHOMOLOGY OF
 $GL_N(\mathbb{Z} )$ FOR
$GL_N(\mathbb{Z} )$ FOR  $N\geqslant 8$ AND THE TRIVIALITY OF
$N\geqslant 8$ AND THE TRIVIALITY OF  $K_8(\mathbb{Z} )$
$K_8(\mathbb{Z} )$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-26
-
- Article
- Export citation
LEVELS OF CANCELLATION FOR MONOIDS AND MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The geometric Satake equivalence for integral motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 17 December 2025, pp. 2755-2851
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant Segre and Verlinde invariants for Quot schemes
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the homology stability range for symplectic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 11 December 2025, pp. 2724-2753
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the formal Peterson subalgebra and its dual
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-BPS categories for symmetric quivers with potential
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 16 September 2025, pp. 1799-1854
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TORSION BIRATIONAL MOTIVES OF SURFACES AND UNRAMIFIED COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 2283-2315
- Print publication:
- November 2025
-
- Article
-
- You have access
- HTML
- Export citation
An analogue of the Milnor conjecture for the de Rham-Witt complex in characteristic 2
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ASYMPTOTIC DIMENSION AND GEOMETRIC DECOMPOSITIONS IN DIMENSIONS 3 AND 4
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 21 April 2025, pp. 176-201
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable homology of Lie algebras of derivations and homotopy invariants of wheeled operads
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 13 August 2025, pp. 756-799
- Print publication:
- April 2025
-
- Article
- Export citation
SIMPLE TYPE THEORY FOR METAPLECTIC COVERS OF
 $\operatorname {GL}(r)$ OVER A NON-ARCHIMEDEAN LOCAL FIELD
$\operatorname {GL}(r)$ OVER A NON-ARCHIMEDEAN LOCAL FIELD
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1263-1335
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ample Groupoids, Topological Full groups, Algebraic K-theory Spectra and Infinite Loop Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 February 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KK-theory of circle actions with the Rokhlin property
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 February 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalised Dirac-Schrödinger operators and the Callias Theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The abelianization of the elementary group of rank two
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 487-505
-
- Article
- Export citation
Semiregularity as a consequence of Goodwillie’s theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 23 December 2024, e126
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RANKS OF SOFT OPERATORS IN NOWHERE SCATTERED
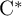 $\mathrm {C}^*$-ALGEBRAS
$\mathrm {C}^*$-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 371-410
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vanishing of Nil-terms and negative K-theory for additive categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1945-2023
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation