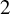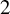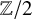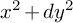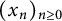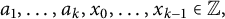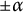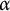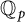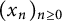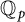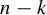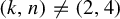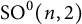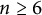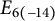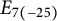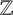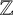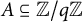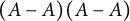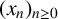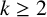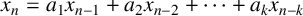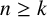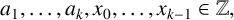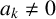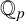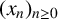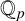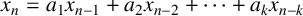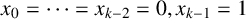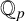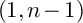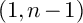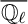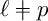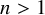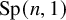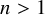Refine listing
Actions for selected content:
114 results in 11Exx
K3 SURFACES AND ORTHOGONAL MODULAR FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 29 August 2025, pp. 687-727
- Print publication:
- December 2025
-
- Article
- Export citation
Unimodular Hunting II
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 August 2025, e136
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RIGID INNER FORMS OVER GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 2181-2256
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An analogue of the Milnor conjecture for the de Rham-Witt complex in characteristic 2
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds on the Pythagoras number and indecomposables in biquadratic fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 31 March 2025, pp. 843-868
-
- Article
- Export citation
COVERING INTEGERS BY
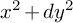 $x^2 + dy^2$
$x^2 + dy^2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 847-889
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXISTENCE OF K-MULTIMAGIC SQUARES AND MAGIC SQUARES OF kth POWERS WITH DISTINCT ENTRIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 441-448
- Print publication:
- December 2025
-
- Article
- Export citation
p-Adic quotient sets: Linear recurrence sequences with reducible characteristic polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 11 December 2024, pp. 177-186
- Print publication:
- March 2025
-
- Article
- Export citation
Equidistribution of rational subspaces and their shapes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 10 November 2023, pp. 2009-2062
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounded cohomology is not a profinite invariant
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 379-390
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE LIFTING PROBLEM FOR UNIVERSAL QUADRATIC FORMS OVER SIMPLEST CUBIC FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 77-89
- Print publication:
- August 2024
-
- Article
- Export citation
On some multiplicative properties of large difference sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 1538-1555
- Print publication:
- October 2024
-
- Article
- Export citation
Finite subgroups of automorphisms of K3 surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 June 2023, e54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REAL TOPOLOGICAL HOCHSCHILD HOMOLOGY OF SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 07 June 2023, pp. 1461-1518
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gabber rigidity in hermitian K-theory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 27 April 2023, pp. 1842-1847
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
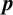 $\boldsymbol {p}$-ADIC QUOTIENT SETS: LINEAR RECURRENCE SEQUENCES
$\boldsymbol {p}$-ADIC QUOTIENT SETS: LINEAR RECURRENCE SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 05 January 2023, pp. 19-28
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COHOMOLOGY OF THE BRUHAT–TITS STRATA IN THE UNRAMIFIED UNITARY RAPOPORT–ZINK SPACE OF SIGNATURE
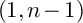 $(1,n-1)$
$(1,n-1)$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 470-497
- Print publication:
- June 2023
-
- Article
- Export citation
Quaternionic hyperbolic lattices of minimal covolume
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 25 August 2022, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number fields without universal quadratic forms of small rank exist in most degrees
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 06 May 2022, pp. 225-231
- Print publication:
- March 2023
-
- Article
- Export citation
Grothendieck–Serre in the quasi-split unramified case
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 29 March 2022, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation