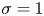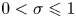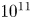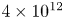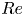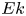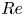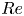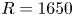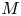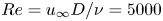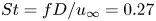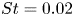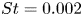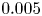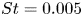Open access
Contents
JFM Papers
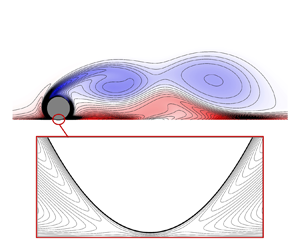
The inner and outer solutions to the inertial flow over a rolling circular cylinder
-
- Published online by Cambridge University Press:
- 04 May 2023, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal control of tidal flow
-
- Published online by Cambridge University Press:
- 04 May 2023, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The buoyancy staircase limit in surface quasigeostrophic turbulence
-
- Published online by Cambridge University Press:
- 04 May 2023, A35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Lagrangian nature of fingering convection
-
- Published online by Cambridge University Press:
- 04 May 2023, A34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Assessing passive scalar dynamics in bubble-induced turbulence using direct numerical simulations
-
- Published online by Cambridge University Press:
- 04 May 2023, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tensor-based flow reconstruction from optimally located sensor measurements
-
- Published online by Cambridge University Press:
- 04 May 2023, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reynolds number scaling and energy spectra in geostrophic convection
-
- Published online by Cambridge University Press:
- 04 May 2023, A36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The role of a pre-wetting layer in resolving the contact line paradox of thin films in infinite elastic domains
-
- Published online by Cambridge University Press:
- 03 May 2023, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transient deformation of a viscoelastic capsule in a cross-slot microchannel: effects of inertia and membrane viscosity
-
- Published online by Cambridge University Press:
- 03 May 2023, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Surface-temperature-induced Marangoni effects on developing buoyancy-driven flow
-
- Published online by Cambridge University Press:
- 02 May 2023, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POD-based study of turbulent plane Poiseuille flow: comparing structure and dynamics between quasi-linear simulations and DNS
-
- Published online by Cambridge University Press:
- 28 April 2023, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effect of flow–thermodynamics interactions on the stability of compressible boundary layers: insights from Helmholtz decomposition
-
- Published online by Cambridge University Press:
- 28 April 2023, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interaction of mode-one internal solitary waves of opposite polarity in double-pycnocline stratifications
-
- Published online by Cambridge University Press:
- 28 April 2023, A17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
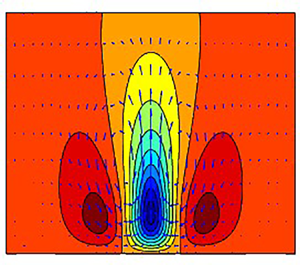
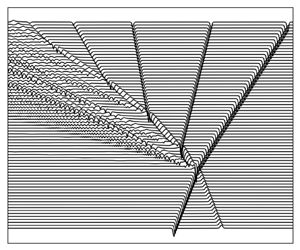
Coherent motions in a turbulent wake of an axisymmetric bluff body
-
- Published online by Cambridge University Press:
- 28 April 2023, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Velocity field and cavity dynamics in drop impact experiments
-
- Published online by Cambridge University Press:
- 28 April 2023, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scaling CO2–brine mixing in permeable media via analogue models
-
- Published online by Cambridge University Press:
- 27 April 2023, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear response analysis of supersonic turbulent channel flows with a large parameter space
-
- Published online by Cambridge University Press:
- 27 April 2023, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vortex-induced vibration forever even with high structural damping
-
- Published online by Cambridge University Press:
- 27 April 2023, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bubble collapse near porous plates
-
- Published online by Cambridge University Press:
- 27 April 2023, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sustainability of the plastron on nano-grass-covered micro-trench superhydrophobic surfaces in high-speed flows of open water
-
- Published online by Cambridge University Press:
- 27 April 2023, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation