 $\ast $-CLEAN RINGS
$\ast $-CLEAN RINGS
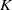 $K$-GROUPS
$K$-GROUPS
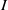 $I$-ADIC COMPLETION
$I$-ADIC COMPLETION
 $\alpha $-LIKE RADICALS OF RINGS
$\alpha $-LIKE RADICALS OF RINGS