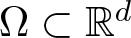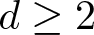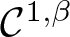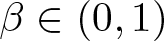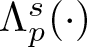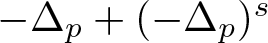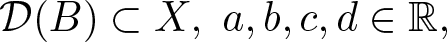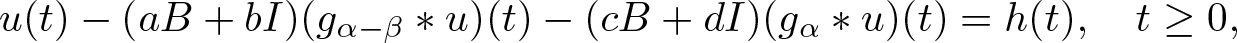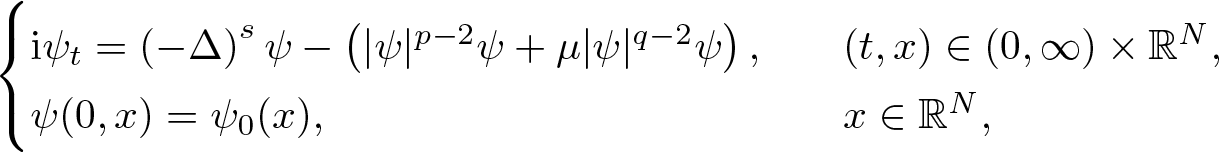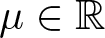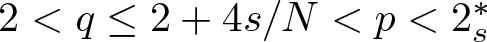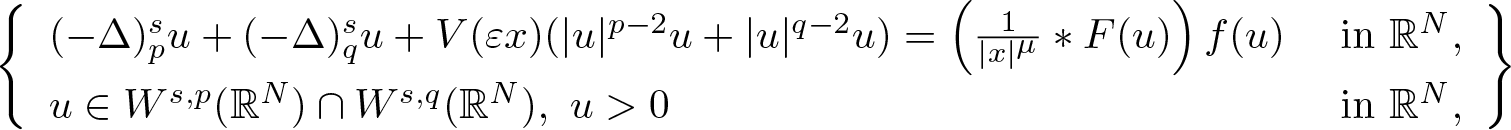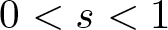Refine listing
Actions for selected content:
218 results in 35Rxx
On global fractional Calderón–Zygmund regularity for the fractional Dirichlet problem on Lipschitz domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-31
-
- Article
- Export citation
STABILITY RESULTS FOR NONLOCAL SERRIN-TYPE PROBLEMS, ANTISYMMETRIC HARNACK INEQUALITIES AND GEOMETRIC ESTIMATES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 04 July 2025, pp. 394-396
- Print publication:
- October 2025
-
- Article
-
- You have access
- HTML
- Export citation
The evolution problem for the 1D nonlocal Fisher-KPP equation with a top hat kernel. Part 2. The initial-boundary value problem on a finite domain
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Correspondence between Pestov and Weitzenböck identities
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 02 May 2025, pp. 443-463
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal transport on gas networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hardy and Rellich Inequalities with Bessel Pairs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 31 March 2025, pp. 825-842
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elliptic Pre-Complexes, Hodge-like Decompositions and Overdetermined Boundary-Value Problems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 March 2025, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Solution theory of fractional SDEs in complete subcritical regimes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strict Faber–Krahn-type inequality for the mixed local–nonlocal operator under polarization
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 506-525
-
- Article
- Export citation
Well-posedness for strongly damped abstract Cauchy problems of fractional order
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-27
-
- Article
- Export citation
Mean field limits of co-evolutionary signed heterogeneous networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 06 January 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NONRELATIVISTIC LIMIT FOR THE TRAVELLING WAVES OF THE PSEUDORELATIVISTIC HARTREE EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 26 December 2024, pp. 172-183
- Print publication:
- August 2025
-
- Article
- Export citation
Fractional time differential equations as a singular limit of the Kobayashi–Warren–Carter system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 December 2024, pp. 1-37
-
- Article
- Export citation
Continuum limit for interacting systems on adaptive networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 06 December 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal stopping of Gauss–Markov bridges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 04 December 2024, pp. 1-34
- Print publication:
- March 2025
-
- Article
- Export citation
SYMMETRY RESTORATION IN COLLISIONS OF SOLITONS IN FRACTIONAL COUPLERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 03 December 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence speed and approximation accuracy of numerical MCMC
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 101-133
- Print publication:
- March 2025
-
- Article
- Export citation
Instability of standing waves for fractional NLS with combined nonlinearities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-29
-
- Article
- Export citation
Global dynamics for the stochastic nonlinear beam equations on the four-dimensional torus
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Concentration and multiplicity of solutions for fractional double phase problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-54
-
- Article
- Export citation