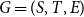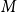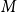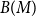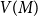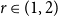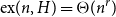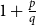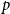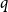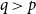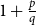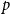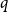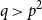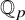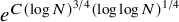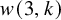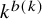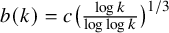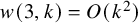Refine listing
Actions for selected content:
22 results in RSS Journal Articles Collection
A BK inequality for random matchings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 22 July 2022, pp. 151-157
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Calabi–Yau properties of Postnikov diagrams
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 July 2022, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On local weak limit and subgraph counts for sparse random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 July 2022, pp. 755-776
- Print publication:
- September 2022
-
- Article
- Export citation
Many Turán exponents via subdivisions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 21 July 2022, pp. 134-150
-
- Article
- Export citation
A note on the polynomial ergodicity of the one-dimensional Zig-Zag process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 18 July 2022, pp. 895-903
- Print publication:
- September 2022
-
- Article
- Export citation
Where are the zeroes of a random p-adic polynomial?
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 18 July 2022, e55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EVALUATING THE TAIL RISK OF MULTIVARIATE AGGREGATE LOSSES
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 52 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 July 2022, pp. 921-952
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New lower bounds for van der Waerden numbers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 July 2022, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An extended class of univariate and multivariate generalized Pólya processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 July 2022, pp. 974-997
- Print publication:
- September 2022
-
- Article
- Export citation
Quadratic Klein-Gordon equations with a potential in one dimension
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 11 July 2022, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large-time behaviour and the second eigenvalue problem for finite-state mean-field interacting particle systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 85-125
- Print publication:
- March 2023
-
- Article
- Export citation
Scalable algorithms for physics-informed neural and graph networks
-
- Journal:
- Data-Centric Engineering / Volume 3 / 2022
- Published online by Cambridge University Press:
- 29 June 2022, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generating weighted and thresholded gene coexpression networks using signed distance correlation
-
- Journal:
- Network Science / Volume 10 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 16 June 2022, pp. 131-145
-
- Article
- Export citation
MORTALITY CREDITS WITHIN LARGE SURVIVOR FUNDS
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 52 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 813-834
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Universal Digital Twin: Integration of national-scale energy systems and climate data
-
- Journal:
- Data-Centric Engineering / Volume 3 / 2022
- Published online by Cambridge University Press:
- 13 June 2022, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bringing network science to primary school
-
- Journal:
- Network Science / Volume 10 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 207-213
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fatty acid composition of milk from mothers giving birth at extremely low gestation in Sweden
-
- Journal:
- Experimental Results / Volume 3 / 2022
- Published online by Cambridge University Press:
- 24 February 2022, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Three-dimensional complex architectures observed in shock processed amino acid mixtures
-
- Journal:
- Experimental Results / Volume 3 / 2022
- Published online by Cambridge University Press:
- 09 February 2022, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AI: Coming of age?
-
- Journal:
- Annals of Actuarial Science / Volume 16 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 19 January 2022, pp. 1-5
-
- Article
-
- You have access
- HTML
- Export citation
Modelling random vectors of dependent risks with different elliptical components
-
- Journal:
- Annals of Actuarial Science / Volume 16 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 22 February 2021, pp. 6-24
-
- Article
- Export citation