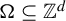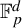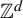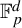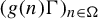Refine listing
Actions for selected content:
387 results in 37Axx
Equidistribution for nilsequences along spheres over finite fields
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 29 December 2025, pp. 1-73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-stationary distributions in reducible state spaces
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 26 December 2025, pp. 1-37
-
- Article
- Export citation
Disintegration results for fractal measures and applications to Diophantine approximation
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 23 December 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the selection of subaction and measure for perturbed potentials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 17 December 2025, pp. 1-35
-
- Article
- Export citation
A threshold for Poisson behavior of non-stationary product measures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On ergodicity and transience for a class of level-dependent GI/M/1-type Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 21 November 2025, pp. 1301-1317
- Print publication:
- December 2025
-
- Article
- Export citation
Some ergodic theorems involving Omega function and their applications
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 17 November 2025, pp. 1-20
-
- Article
-
- You have access
- HTML
- Export citation
ON THE SHORTEST DISTANCE BETWEEN ORBITS IN CONFORMAL ITERATED FUNCTION SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-11
-
- Article
- Export citation
KATSURA–EXEL–PARDO SELF-SIMILAR ACTIONS, PUTNAM’S BINARY FACTORS AND THEIR LIMIT SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 31 October 2025, pp. 382-417
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MORPHISMS OF CUNTZ–PIMSNER ALGEBRAS FROM COMPLETELY POSITIVE MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 31 October 2025, pp. 274-313
- Print publication:
- December 2025
-
- Article
- Export citation
Revisiting sums and products in countable and finite fields
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large deviations for occupation and waiting times of infinite ergodic transformations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $\overline {d}$-continuity for countable state shifts
$\overline {d}$-continuity for countable state shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1-24
-
- Article
- Export citation
Continuity of the orthogeodesic foliation and ergodic theory of the earthquake flow
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 September 2025, e151
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Almost sure convergence of cover times for
 $\psi $-mixing systems
$\psi $-mixing systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 19 September 2025, pp. 320-336
- Print publication:
- January 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Variational principles of metric mean dimension for random dynamical systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 September 2025, pp. 1-25
-
- Article
-
- You have access
- HTML
- Export citation
A new class of α-Farey maps and an application to normal numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quenched decay of correlations for random contracting Lorenz maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-58
-
- Article
- Export citation
Quantitative ergodic theorems for actions of groups of polynomial growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 04 September 2025, pp. 128-181
- Print publication:
- January 2026
-
- Article
- Export citation
Pointwise convergence of bilinear polynomial averages over the primes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 01 September 2025, pp. 3760-3799
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation