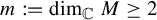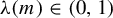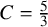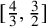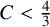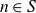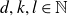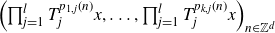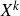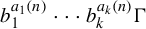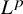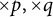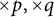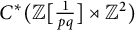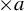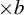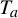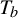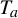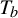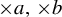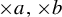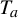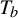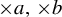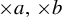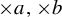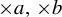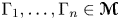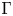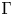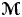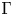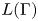Refine listing
Actions for selected content:
387 results in 37Axx
On the ergodicity of unitary frame flows on Kähler manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 16 October 2023, pp. 2143-2172
- Print publication:
- August 2024
-
- Article
- Export citation
Low complexity subshifts have discrete spectrum
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 12 October 2023, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exponential multiple mixing for commuting automorphisms of a nilmanifold
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 1729-1740
- Print publication:
- July 2024
-
- Article
- Export citation
Multiple recurrence and popular differences for polynomial patterns in rings of integers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 239-278
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pointwise convergence in nilmanifolds along smooth functions of polynomial growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 1963-2008
- Print publication:
- July 2024
-
- Article
- Export citation
On a multi-parameter variant of the Bellow–Furstenberg problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 September 2023, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Measure-theoretic sequence entropy pairs and mean sensitivity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 19 September 2023, pp. 1531-1540
- Print publication:
- June 2024
-
- Article
- Export citation
Spectral cocycle for substitution tilings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 18 September 2023, pp. 1629-1672
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strongly mixing systems are almost strongly mixing of all orders
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 13 September 2023, pp. 1489-1530
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On some multiplicative properties of large difference sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 1538-1555
- Print publication:
- October 2024
-
- Article
- Export citation
A tracial characterization of Furstenberg’s
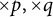 $\times p,\times q$ conjecture
$\times p,\times q$ conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 06 September 2023, pp. 244-256
- Print publication:
- March 2024
-
- Article
- Export citation
A nonconservative kinetic framework under the action of an external force field: Theoretical results with application inspired to ecology
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 31 August 2023, pp. 1170-1186
-
- Article
- Export citation
Adaptation of a population to a changing environment in the light of quasi-stationarity
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 30 August 2023, pp. 235-286
- Print publication:
- March 2024
-
- Article
- Export citation
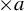 $\times a$ and
$\times a$ and 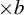 $\times b$ empirical measures, the irregular set and entropy
$\times b$ empirical measures, the irregular set and entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 1673-1692
- Print publication:
- June 2024
-
- Article
- Export citation
Measure equivalence rigidity via s-malleable deformations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 14 August 2023, pp. 2023-2050
- Print publication:
- October 2023
-
- Article
- Export citation
Sharp constants in inequalities admitting the Calderón transference principle
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 04 August 2023, pp. 1597-1608
- Print publication:
- June 2024
-
- Article
- Export citation
Orbits closeness for slowly mixing dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1192-1208
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuum of allosteric actions for non-amenable surface groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 19 July 2023, pp. 1581-1596
- Print publication:
- June 2024
-
- Article
- Export citation
Statistical aspects of mean field coupled intermittent maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 19 July 2023, pp. 945-957
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CURVATURE-TORSION ENTROPY FOR TWISTED CURVES UNDER CURVE SHORTENING FLOW
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 11 July 2023, pp. 571-580
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation