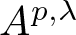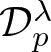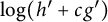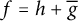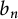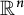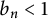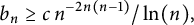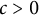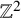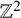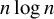Refine listing
Actions for selected content:
111 results in 31xxx
Harmonic exponential terms are polynomial
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 09 October 2025, pp. 1-6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Note on real and imaginary parts of harmonic quasiregular mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 25 September 2025, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Normalized ground states for a biharmonic Choquard equation with exponential critical growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 September 2025, pp. 1-35
-
- Article
- Export citation
Phragmén–Lindelöf principles and Julia limiting directions of quasiregular mappings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 11 June 2025, pp. 3325-3343
- Print publication:
- November 2025
-
- Article
- Export citation
On a convergence of positive continuous additive functionals in terms of the smooth measures
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 May 2025, pp. 1-30
-
- Article
- Export citation
MIXED BOUNDARY VALUE PROBLEM IN MICROFLUIDICS: THE AVER’YANOV–BLUNT MODEL REVISITED
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 07 April 2025, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elliptic Pre-Complexes, Hodge-like Decompositions and Overdetermined Boundary-Value Problems
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 March 2025, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A sharp threshold for Trudinger–Moser type inequalities with logarithmic kernels in dimension N
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-39
-
- Article
- Export citation
ON MARCH’S CRITERION FOR TRANSIENCE ON ROTATIONALLY SYMMETRIC MANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 323-333
- Print publication:
- October 2025
-
- Article
- Export citation
On boundary-non-preserving mappings with Poletsky inequality
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 834-855
- Print publication:
- September 2025
-
- Article
- Export citation
Schwarz lemma for harmonic functions in the unit ball
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 616-633
-
- Article
- Export citation
Complex linear differential equations with solutions in weighted Dirichlet spaces and derivative Hardy spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 06 January 2025, pp. 653-666
- Print publication:
- September 2025
-
- Article
- Export citation
Finely quasiconformal mappings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-25
-
- Article
- Export citation
Cesàro-type operators on Bergman–Morrey spaces and Dirichlet–Morrey spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 268-299
-
- Article
- Export citation
Dirichlet-type spaces of the unit bidisc and toral 2-isometries
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1271-1293
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonlocal anisotropic interactions of Coulomb type
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1677-1707
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral mean estimates for univalent and locally univalent harmonic mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 15 January 2024, pp. 655-669
- Print publication:
- September 2024
-
- Article
- Export citation
Systems involving mean value formulas on trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 03 January 2024, pp. 351-383
- Print publication:
- April 2025
-
- Article
- Export citation
Lower bounds on Bourgain’s constant for harmonic measure
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1967-1986
- Print publication:
- December 2024
-
- Article
- Export citation
Collapse and diffusion in harmonic activation and transport
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 September 2023, e85
-
- Article
-
- You have access
- Open access
- HTML
- Export citation