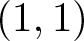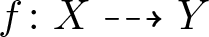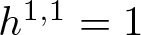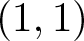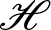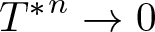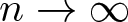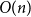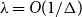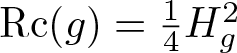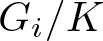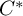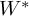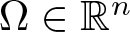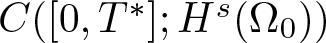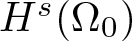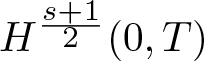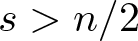Refine search
Actions for selected content:
25814 results in Abstract analysis
The admissible KMS bundles on classifiable C⁎-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 November 2024, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert type operators acting from the Bloch space into Bergman spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 205-225
-
- Article
- Export citation
Moishezon manifolds with no nef and big classes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 198-204
-
- Article
- Export citation
Cesàro-type operators on Bergman–Morrey spaces and Dirichlet–Morrey spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 268-299
-
- Article
- Export citation
Fractal interpolant curve fitting and reproducing kernel Hilbert spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 247-267
-
- Article
- Export citation
Kolmogorov’s theorem for degenerate Hamiltonian systems with Hölder continuous parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-36
-
- Article
- Export citation
Well-posedness of quasilinear parabolic equations in time-weighted spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-33
-
- Article
- Export citation
Minimal isometric dilations and operator models for the polydisc
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-40
-
- Article
- Export citation
Geometry of tropical extensions of hyperfields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal mixing via tensorization for random independent sets on arbitrary trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 259-275
-
- Article
- Export citation
Generalized Ricci flow on aligned homogeneous spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 226-246
-
- Article
- Export citation
Equivariant parametrized topological complexity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-24
-
- Article
- Export citation
Semiabelian varieties and transcendence on Weierstrass sigma functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 107-113
- Print publication:
- January 2025
-
- Article
- Export citation
Local regularity for nonlocal double phase equations in the Heisenberg group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-37
-
- Article
- Export citation
RIGIDITY FOR VON NEUMANN ALGEBRAS OF GRAPH PRODUCT GROUPS II. SUPERRIGIDITY RESULTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 117-156
- Print publication:
- January 2025
-
- Article
- Export citation
An MBO method for modularity optimisation based on total variation and signless total variation
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enlargements and Morita contexts for rings with involution
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 131-162
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Riemann–Hilbert problem and multiple high-order pole solutions to the cubic Camassa–Holm equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-51
-
- Article
- Export citation
Dynamics of projectable functions: towards an atlas of wandering domains for a family of Newton maps
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Radial solutions of initial boundary value problems of nonlinear Schrödinger equations in ℝn
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation