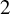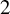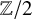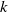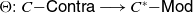Refine listing
Actions for selected content:
454 results in 13xxx
Intersection Theorem for DG-modules over non-positive DG-rings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 12 December 2025, pp. 1-18
-
- Article
- Export citation
COHOMOLOGICAL INTEGRALITY FOR WEAKLY SYMMETRIC REPRESENTATIONS OF REDUCTIVE GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 03 December 2025, pp. 1-37
-
- Article
-
- You have access
- HTML
- Export citation
Polynomial invariants for three-dimensional Leibniz algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 25 November 2025, pp. 1-20
-
- Article
- Export citation
Signature maps from positive cones on algebras with involution
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 November 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pathological MMP singularities as αp-quotients
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 November 2025, e185
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the relevant domain of the Hilbert function of a finite multiprojective scheme
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-31
-
- Article
- Export citation
Silting, cosilting and extensions of commutative rings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 27 October 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Harmonic exponential terms are polynomial
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 09 October 2025, pp. 1-6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hartshorne’s question on cofiniteness of complexes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 07 October 2025, pp. 1-14
-
- Article
- Export citation
ON THE TRIVIALITY OF AN
 $\mathbb A^2$-FIBRATION OVER A DVR
$\mathbb A^2$-FIBRATION OVER A DVR
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 12 September 2025, pp. 826-832
- Print publication:
- December 2025
-
- Article
- Export citation
On coefficient modules of arbitrary modules
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-22
-
- Article
- Export citation
Regularity and multiplicity of Veronese type algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
G-dimensions for DG-modules over commutative DG-rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1370-1389
-
- Article
- Export citation
Ideals and their Fitting ideals
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 30 July 2025, pp. 609-621
- Print publication:
- November 2025
-
- Article
- Export citation
Consistent dimer models on surfaces with boundary
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE REGULARITY INDEX OF FAT POINTS WHOSE SUPPORT IS CONTAINED IN A LINEAR PROPER SUBSPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-8
-
- Article
- Export citation
Locally compact modules over abelian groups and compactly generated metabelian groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1250-1283
- Print publication:
- June 2025
-
- Article
- Export citation
Functional degrees and arithmetic applications III: beyond prime exponent
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 30 May 2025, pp. 409-438
- Print publication:
- September 2025
-
- Article
- Export citation
An analogue of the Milnor conjecture for the de Rham-Witt complex in characteristic 2
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Homological full-and-faithfulness of comodule inclusion and contramodule forgetful functors
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 21 May 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation