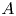Refine listing
Actions for selected content:
103 results in 35Pxx
Linear damping estimates for periodic roll wave solutions of the inviscid Saint-Venant equations and related systems of hyperbolic balance laws
- Part of
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 05 December 2025, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp bounds for higher Steklov–Dirichlet eigenvalues on domains with spherical holes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-20
-
- Article
- Export citation
Constructing surfaces with first Steklov eigenvalue of arbitrarily large multiplicity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp Hardy and spectral gap inequalities on special irreversible Finsler manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-36
-
- Article
- Export citation
Existence of minimizers of the stability constant of Caffarelli–Kohn–Nirenberg inequality
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-23
-
- Article
- Export citation
The inverse scattering theory of Kadomtsev–Petviashvili II equations
- Part of
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 04 August 2025, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characters and transfer maps via categorified traces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 June 2025, e93
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral ratios and gaps for Steklov eigenvalues of balls with revolution-type metrics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 14 January 2025, pp. 492-511
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lp positivity preservation and self-adjointness of Schrödinger operators on incomplete Riemannian manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral asymptotics for linear elasticity: the case of mixed boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized second order vectorial ∞-eigenvalue problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 27 March 2024, pp. 2150-2170
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral theory of the invariant Laplacian on the disk and the sphere – a complex analysis approach
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 01 March 2024, pp. 940-974
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On generalized eigenvalue problems of fractional (p, q)-Laplace operator with two parameters
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 22 January 2024, pp. 1385-1430
- Print publication:
- August 2025
-
- Article
- Export citation
A universal inequality for Neumann eigenvalues of the Laplacian on a convex domain in Euclidean space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 19 September 2023, pp. 222-226
- Print publication:
- March 2024
-
- Article
- Export citation
On the linearized Whitham–Broer–Kaup system on bounded domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 104-123
- Print publication:
- February 2025
-
- Article
- Export citation
The Lp convergence of Fourier series on triangular domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 453-474
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
General kernel estimates of Schrödinger-type operators with unbounded diffusion terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 19 May 2023, pp. 929-960
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REILLY-TYPE UPPER BOUNDS FOR THE p-STEKLOV PROBLEM ON SUBMANIFOLDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 492-503
- Print publication:
- December 2023
-
- Article
- Export citation
On Duclos–Exner’s conjecture about waveguides in strong uniform magnetic fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 February 2023, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shape sensitivity of the Hardy constant involving the distance from a boundary submanifold
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 22 February 2023, pp. 408-423
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation













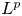
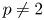
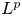




 of the “complexified unit circle”
of the “complexified unit circle”