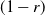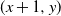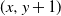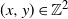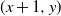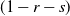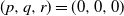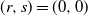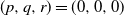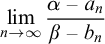Refine listing
Actions for selected content:
126 results in 68Qxx
Generalized percolation games on the two-dimensional square lattice and ergodicity of associated probabilistic cellular automata
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 06 February 2026, pp. 1-97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform convergence of adversarially robust classifiers
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 37 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 24 November 2025, pp. 43-72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On approximating the Potts model with contracting Glauber dynamics
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 07 November 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENDING THE BARMPALIAS–LEWIS-PYE LIMIT THEOREM TO ALL REALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 28 October 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The group of reversible turing machines: subgroups, generators, and computability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 October 2025, e176
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on the computational complexity of weak saturation
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 35 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 16 October 2025, pp. 83-88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RATE OF CONVERGENCE OF COMPUTABLE PREDICTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The complexity of intersecting subproducts with subgroups in Cartesian powers
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 07 October 2025, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vanishing of Schubert coefficients via the effective Hilbert nullstellensatz
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 01 October 2025, e162
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Adversarial flows: A gradient flow characterization of adversarial attacks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 37 / Issue 1 / February 2026
- Published online by Cambridge University Press:
- 12 September 2025, pp. 123-179
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Online matching for the multiclass stochastic block model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1360-1381
- Print publication:
- December 2025
-
- Article
- Export citation
MICRO-MACRO PARAREAL, FROM ORDINARY DIFFERENTIAL EQUATIONS TO STOCHASTIC DIFFERENTIAL EQUATIONS AND BACK AGAIN
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 17 March 2025, e13
-
- Article
- Export citation
On the algorithmic descriptive complexity of attractors in topological dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 2533-2560
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A MODULAR BISIMULATION CHARACTERISATION FOR FRAGMENTS OF HYBRID LOGIC
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 590-618
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LEARNING EQUIVALENCE RELATIONS ON POLISH SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 February 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE COMPLEXITY OF ORDER-COMPUTABLE SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 24 January 2025, pp. 1-24
-
- Article
- Export citation
The promise of neuromorphic edge AI for rural environmental monitoring
- Part of
-
- Journal:
- Environmental Data Science / Volume 3 / 2024
- Published online by Cambridge University Press:
- 02 January 2025, e34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sampling from the random cluster model on random regular graphs at all temperatures via Glauber dynamics
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 09 December 2024, pp. 359-391
-
- Article
- Export citation
Equality cases of the Alexandrov–Fenchel inequality are not in the polynomial hierarchy
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 November 2024, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A PARAMETERIZED HALTING PROBLEM,
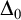 $ \Delta _0$ TRUTH AND THE MRDP THEOREM
$ \Delta _0$ TRUTH AND THE MRDP THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 483-508
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation