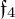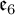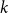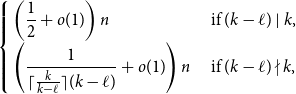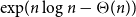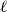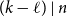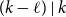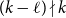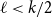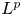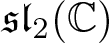Refine search
Actions for selected content:
25814 results in Abstract analysis
Contents
-
- Book:
- Functional Analysis Revisited
- Published online:
- 31 October 2024
- Print publication:
- 04 July 2024, pp v-viii
-
- Chapter
- Export citation
15 - We Go Deeper, DeeperWe Go (into the Structure of Complete Spaces)
-
- Book:
- Functional Analysis Revisited
- Published online:
- 31 October 2024
- Print publication:
- 04 July 2024, pp 185-209
-
- Chapter
- Export citation
8 - Norms Do Differ
-
- Book:
- Functional Analysis Revisited
- Published online:
- 31 October 2024
- Print publication:
- 04 July 2024, pp 78-87
-
- Chapter
- Export citation
EXCEPTIONAL SIMPLE REAL LIE ALGEBRAS
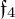 $\mathfrak {f}_4$ AND
$\mathfrak {f}_4$ AND 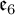 $\mathfrak {e}_6$ VIA CONTACTIFICATIONS
$\mathfrak {e}_6$ VIA CONTACTIFICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 July 2024, pp. 157-201
- Print publication:
- January 2025
-
- Article
- Export citation
JMJ volume 23 issue 4 Cover and Front matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. f1-f2
- Print publication:
- July 2024
-
- Article
-
- You have access
- Export citation
JMJ volume 23 issue 4 Cover and Back matter
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. b1-b2
- Print publication:
- July 2024
-
- Article
-
- You have access
- Export citation
Equisingularity in pencils of curves on germs of reduced complex surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 04 June 2024, pp. 990-1012
-
- Article
- Export citation
Rigidity for the perimeter inequality under Schwarz symmetrization
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting spanning subgraphs in dense hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 30 May 2024, pp. 729-741
-
- Article
- Export citation
The homotopy decomposition of the suspension of a non-simply-connected five-manifold – ADDENDUM
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 May 2024, p. 1
-
- Article
- Export citation
On a class of self-similar sets which contain finitely many common points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-22
-
- Article
- Export citation
Maintenance of steady-state mRNA levels by a microRNA-based feed forward loop in the presence of stochastic gene expression noise
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 29 May 2024, pp. 143-160
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A generalisation of Varnavides’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 29 May 2024, pp. 724-728
-
- Article
- Export citation
Lp positivity preservation and self-adjointness of Schrödinger operators on incomplete Riemannian manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A classification of automorphic Lie algebras on complex tori
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 28 May 2024, pp. 947-989
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distribution in homology classes and discrete fractal dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 May 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COHOMOLOGIE DE DE RHAM DU REVÊTEMENT MODÉRÉ DE L’ESPACE DE DRINFELD
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 28 May 2024, pp. 2733-2775
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral asymptotics for linear elasticity: the case of mixed boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED GAN–GROSS–PRASAD CONJECTURE FOR CERTAIN TEMPERED L-PACKETS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 May 2024, pp. 17-39
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Appendix C - Coupling and Total Variation
-
- Book:
- Harmonic Functions and Random Walks on Groups
- Published online:
- 16 May 2024
- Print publication:
- 23 May 2024, pp 370-373
-
- Chapter
- Export citation